Οι αρχές της πυθαγόρειας φιλοσοφίας
ΠΡΩΤΗ ΔΗΜΟΣΙΕΥΣΗ
Από τον Αναστάσιο Ν. Πανά
Μικρός περίπατος στα πυθαγόρεια μαθηματικά, κοσμολογία και αστρονομία, και στις σύγχρονες προεκτάσεις τους.
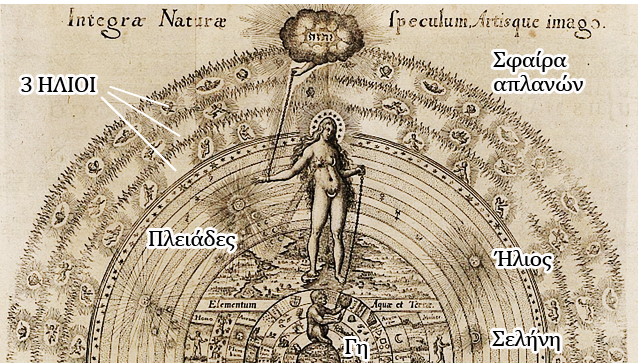
Σχέδιο του 1574 με την Ψυχή του Κόσμου (Anima Mundi) και τη διάταξη των κόσμων σύμφωνα με την πυθαγόρεια κοσμοθεώρηση. Πάνω στη Γη κάθεται ένας πίθηκος που κρατά μια ουράνια σφαίρα. Πηγή: Supplied
v
Ο ΠΥΘΑΓΟΡΑΣ δεν είναι μόνο γνωστός για τις μετενσαρκώσεις του, αλλά και για μερικά άλλα πράγματα, που αποτελούσαν καινοτομίες στην εποχή του και για τα οποία προκάλεσε τον φθόνο των συγχρόνων του. Για παράδειγμα, αυτός ανακάλυψε πρώτος αυτό που ονομάζουμε «οικονομικό σύστημα», καθιερώνοντας το νόμισμα ως μέσο συναλλαγής. Αυτός επίσης πρώτος μίλησε για την «αρμονία των σφαιρών», δηλαδή τις μαθηματικές σχέσεις που συνδέουν τον γήινο κόσμο με τη Σελήνη και τον Ήλιο και τους γνωστούς τότε πλανήτες (Ερμή, Αφροδίτη, Άρη, Δία και Κρόνο) με τη σφαίρα των απλανών, απ’ όπου προκύπτουν τα μουσικά διαστήματα σε επτά μέρη, με μια διπλή γεωμετρική πρόοδο με λόγο 2 και λόγο 3, φτάνοντας τελικά στη «μουσική κλίμακα» που γνωρίζουμε σήμερα, με τον συντελεστή 2 να σχηματίζει τις διαδοχικές όγδοες (1, 2, 4, 8…), ενώ η πρόοδος με τον συντελεστή 3 σχηματίζει τις καθαρές δωδεκάτες (1 = ντο , 3 = σολ, 9 = ρε, 27 = λα, 81 = μι…). Η διαπλοκή δύο μόνο αριθμών καθορίζει την αρμονία του κόσμου: του πρώτου ζυγού 2 και του πρώτου περιττού 3, των δυνάμεών τους και των αντίστοιχων λόγων τους. Και επειδή τα πάντα στο σύμπαν είναι αριθμοί, τα πάντα αναβλύζουν αρμονία.
Γι’ αυτό το λόγο ο Πλάτωνας βάζει στο στόμα ενός πυθαγόρειου τη φράση: «ο κόσμος βρίσκεται εξ ολοκλήρου υπό το κράτος της αρμονίας». Πρόκειται για την «ψυχή του κόσμου», όπως την αποκαλεί ο Τίμαιος∙ αυτή την anima mundi, την Παγκόσμια Ψυχή, την μοιράζονται όλα τα πλάσματα της δημιουργίας.
v
Τα μαθηματικά της Χρυσής Τομής
Όπως έλεγε ο Πυθαγόρας σχετικά με τη δημιουργία του κόσμου, τα πάντα είναι αριθμός: «αριθμός δε, καθάπερ είρηται, τον όλον ουρανόν» (Αριστ. Μετά τα Φυσικά, Α, 5, 986a). Αρχικά υπήρχε το δίπολο άπειρο και πέρας. Από εισπνοή του απείρου, διασπάστηκε το πέρας και από τη μονάδα δημιουργήθηκε η δυάδα και όλοι οι άλλοι αριθμοί.
Και ο Διογένης Λαέρτιος θα συμπληρώσει (Η, 25):
Αρχήν μεν των απάντων μονάδα, εκ δε της μονάδος αόριστον δυάδα, ως αν ύλην τη μονάδι αιτίω όντι υποστήναι∙ εκ δε της μονάδος και της αορίστου δυάδος τους αριθμούς, εκ δε των αριθμών τα σημεία, εκ δε τούτων τα γραμμάς, εξ ων τα επίπεδα σχήματα, εκ δε τούτων τα στερεά σώματα, ων και τα στοιχεία είναι τέτταρα, πυρ, ύδωρ, γην, αέρα…
Οι γεωμετρικές σχέσεις των δύο πρώτων αριθμών, του 2 και του 3, μας δίνουν την ακολουθία Φιμπονάτσι (Fibonacci), μέσα στην οποία κάθε αριθμός είναι το άθροισμα των προηγουμένων: 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144… Επειδή η ακολουθία Φιμπονάτσι παρεμβαίνει σε μεγάλο αριθμό φυσικών φαινομένων, από τη γονιμότητα των ζευγών των κουνελιών (ή των ανθρώπων, πράγμα που είναι το ίδιο), πάνω στην οποία δούλεψε ο Ιταλός μαθηματικός τον 13ο αιώνα, έως τη διάταξη των φύλλων στους μίσχους των φυτών και των φολίδων στο κουκουνάρι, αρκετοί ερμηνευτές θεώρησαν ότι μπορούσαν να διαγνώσουν μέσα στη χρυσή τομή και την πενταγωνική συμμετρία της την περιοδικότητα που χαρακτηρίζει τις ζωντανές μορφές.
Με άλλα λόγια, αν περιέχει μέσα της το κελιδί της αθανασίας.
Ο Πολύκλειτος από τη Σικυώνα (ή το Άργος), αρχιτέκτονας και ανδριαντοποιός σύγχρονος του Φειδία, αναμφίβολα πυθαγόρειας καταγωγής, φαίνεται να χρησιμοποίησε την αναλογία αυτή (5:3) στα μείζονα έργα του: τον Κανόνα ή Δορυφόρο και τον Διαδούμενο.
v

Αριστερά: Ο Δορυφόρος του Πολυκλείτου. Το ανθρώπινο κάλλος πηγάζει
από την συμμετρία των μερών του σώματος. (Γι’ αυτό και το έργο ονομάσθηκε Κανών,
επειδή χρησίμευε ως γνώμονας για τους τότε και μετέπειτα καλλιτέχνες). Ρωμαϊκό αντίγραφο,
Εθνικό Αρχαιολογικό Μουσείο της Νάπολης. Δεξιά: Ο Διαδούμενος (αθλητής δένοντας ταινία
στο κεφάλι του). Εθνικό Αρχαιολογικό Μουσείο της Αθήνας. Πηγή: Wikimedia Commons
v
Σύμφωνα με τον Γαληνό (Περί δογμάτων, 425, 14) ο Πολύκλειτος έγραψε μια πραγματεία που έφερε το ίδιο όνομα με το άγαλμά του, τον Κανόνα, όπου αποκαλύπτει ότι «η αρμονία του σώματος επιτυγχάνεται με τη συμμετρία των αναλογιών του δακτύλου με ενός άλλου δακτύλου, του συνόλου των δακτύλων με του μετακάρπιου και του καρπού, αυτών με του πήχη, του πήχη με τον βραχίονα και όλων με όλα».
Κατά τον Γαληνό πάντα, είχε γράψει ότι «το κάλλος έγκειται στη συμμετρία όλων των μερών». Ο Φίλων ο Μηχανικός (150 π.Χ.), από την άλλη μεριά, του αποδίδει έναν κατεξοχήν πυθαγόρειο συλλογισμό: «Η τελειότητα επιτυγχάνεται το εγγύτερον χάρη σε πολυάριθμους υπολογισμούς» (Mechanicae syntaxis, IV, 2, 50, 5).
Ουσιαστικά, ο Κανόνας του Πολύκλειτου δεν ήταν τίποτε άλλο από την εφαρμογή ατο ανθρώπινο σώμα των αναλογιών της Χρυσής Τομής – μια ακόμη πυθαγόρεια ανακάλυψη. Αυτή η sectio aurea ή proportio divina (χρυσός λόγος ή θεία αναλογία) λέει με απλά λόγια το εξής: δύο μεγέθη έχουν αναλογία χρυσής τομής όταν ο λόγος του αθροίσματός τους (φ) είναι ίσος με το λόγο του μεγαλύτερου μεγέθους (1) προς το μικρότερο (φ-1).
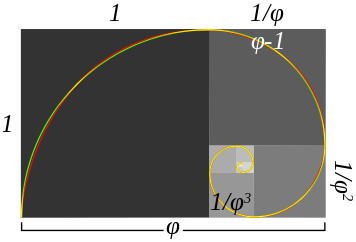 Το μήκος της πλευράς ενός τετραγώνου διαιρούμενο με αυτό του επόμενου
Το μήκος της πλευράς ενός τετραγώνου διαιρούμενο με αυτό του επόμενου
μικρότερου τετραγώνου μας δίνει τη χρυσή αναλογία. Πηγή: Wikimedia Commons
v

Πολλές από τις αναλογίες του Παρθενώνα εκφράζουν τη χρυσή τομή. Πηγή: Wikimedia Commons
v
Στον δυτικό κόσμο, η Χρυσή Τομή θα γίνει διάσημη κυρίως με το έργο De divina proportione (1509) του μαθηματικού Λούκα Πατσιόλι, που εικονογραφήθηκε από τον Λεονάρντο ντα Βίντσι και όπου ο στοχασμός του συγγραφέα στρέφεται γύρω από το πλατωνικό δωδεκάεδρο.
v
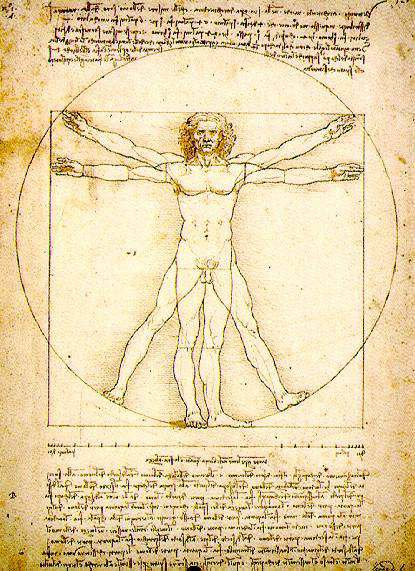
Σελίδα από το βιβλίο De divina proportione (1509) του Λούκα Πατσιόλι
με τον περίφημο «Άνθρωπο του Βιτρούβιου» του Λεονάρντο ντα Βίντσι. Πηγή: Supplied
v
Προσδιορισμένη στις αρχές του 20ού αιώνα με το γράμμα Φ (από το όνομα του Φειδία), η χρυσή τομή προέρχεται από την ακολουθία Φιμπονάτσι, και τούτο διότι οι αμοιβαίοι λόγοι δύο τυχαίων διαδοχικών λόγων της είναι τέτοιοι ώστε να τείνουν προς δύο όρια: 0,618 033 98875… και 1,618 133 98875… προσεγγίζοντας έτσι το λόγο της χρυσής τομής. (Πρακτικά 2:3 ή 5:3· αν δηλαδή διαιρέσουμε ένα μέγεθος σε πέντε μέρη, στα 3/5 περίπου βρίσκεται η χρυσή τομή).
Στα μαθηματικά, ο τύπος της χρυσής τομής εξάγεται από την εξίσωση
v
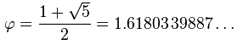
θετική ρίζα, και
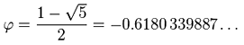
αρνητική ρίζα.
Η αναλογία αυτή, που μας δίνει τη δυνατότητα να διαιρέσουμε μια ευθεία σε μέσο και άκρο λόγο, έτσι ώστε α/β = α + β/α,
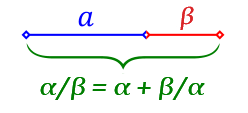
θα συναρπάσει πάμπολλα μυαλά από τον Πλάτωνα έως τον Βοήθιο και από τον Αγρίππα φον Νετεσχάιμ έως τον Λούκα Πατσιόλι φτάνοντας έως τον Λε Κορμπυζιέ και τον δικό του Κανόνα (Modulor) που αποτελεί τη βάση της σύγχρονης αρχιτεκτονικής. (Βλ. Σημείωση στον Λε Κορμπυζιέ στο τέλος του άρθρου).
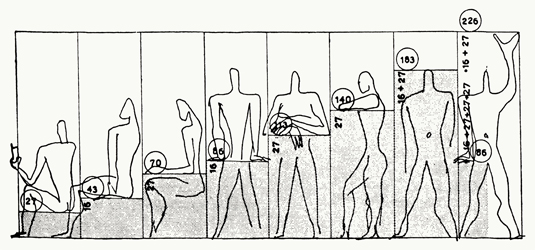 Ο άνθρωπος σε διάφορες στάσεις αποτέλεσε τον Κανόνα (Modulor) του Λε Κορμπυζιέ,
Ο άνθρωπος σε διάφορες στάσεις αποτέλεσε τον Κανόνα (Modulor) του Λε Κορμπυζιέ,
με βάση τον οποίο φτιάχνονται τα σύγχρονα κτίρια. Ο Ελβετός αρχιτέκτονας
μελέτησε τον Παρθενώνα και τις αρμονικές αναλογίες που εκφράζει. Πηγή: Supplied
v

Σχέδιο του Λε Κορμπυζιέ από την επίσκεψή του στην Ακρόπολη και μεταφορά των αναλογιών
της χρυσής τομής (σχήμα επάνω) στον άνθρωπο (δεξιά). Πηγή: Supplied
v
Δεν θα ήταν επομένως υπερβολή αν αποκαλούσαμε όλες αυτές τις διάνοιες πυθαγόρειους και «μαθητές» του Πυθαγόρα.
v
Η πυθαγόρεια κοσμολογία
Ήταν επόμενο οι πυθαγόρειοι να εφαρμόσουν τις γνώσεις τους στα μαθηματικά σε ολόκληρο τον κόσμον, δεδομένου ότι η αστρονομία και η αρμονία είναι όντως «αδελφαί επιστήμαι», όπως θα καταδείξει ο Πλάτωνας στην Πολιτεία (Ζ, 530 d). Η αναγωγή των μουσικών διαστημάτων και των κινήσεων των άστρων σε σταθερές αριθμητικές σχέσεις είχε παρεπόμενο τη διατύπωση της υπόθεσης περί της «αρμονίας των σφαιρών», που πρωτοεμφανίζεται στον Πλάτωνα. (Πολιτεία Ι, 617 b. Πρβλ. Αριστοτέλη, Περί ουρανού Β 9). Εφόσον τα ουράνια σώματα, με υπερμεγέθη μάζα, κινούνται μέσα στον αιθέρα σύμφωνα με κανονικούς νόμους, θα πρέπει να παράγουν επίσης υπερμεγέθεις ήχους, που συνηχούν ανάλογα με τις αντίστοιχες αποστάσεις και ταχύτητές τους στο εσωτερικό της οκτάβας.
Η αντιστοιχία ανάμεσα στα διαστήματα των 7 φθόγγων της μουσικής κλίμακας, που παίζονται στις 7 χορδές της λύρας, και στις αποστάσεις των 7 σωμάτων (των πέντε γνωστών πλανητών, του Ήλιου και της Σελήνης) από τη Γη δημιουργεί ένα κοσμικό επτάχορδο, που ενίσχυε την ενόραση εκείνη, σύμφωνα με την οποία οι αριθμοί κυβερνούν όλα τα επίπεδα της πραγματικότητας, ακόμη και τα πλέον απομακρυσμένα.
Μια ακόμη επανάσταση. Ο πυθαγορισμός αφήνει πίσω του τη διαπλοκή των αισθητών φαινομένων και αντικαθιστά την παραδοσιακή κοσμολογία, που θεωρούσε τη Γη το κέντρο του κόσμου, με μια μαθηματική κοσμολογία που προετοιμάζει το έδαφος για τον ηλιοκεντρισμό, πολύ πριν από τον Γερμανό φιλόσοφο του 15ου αιώνα Νικόλαο Κουζάνο και τον Κοπέρνικο. Ο Πυθαγόρας δίδασκε την σφαιρικότητα της Γης και του κόσμου, βασίζοντάς την όχι σε εμπειρικές παρατηρήσεις (την περίμετρο της σκιάς κατά τη διάρκεια των εκλείψεων, λόγου χάρη) αλλά σε λόγους αρμονικής τάξεως, μια και η σφαίρα είναι το ωραιότερο των στερεών.
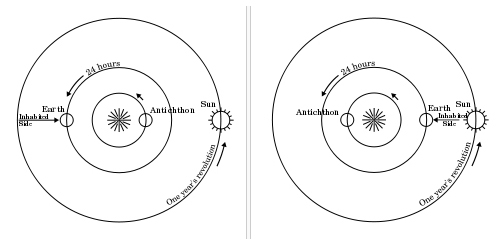 Η Αντιγή (Αντίχθων) ήταν, σύμφωνα με τον Φιλόλαο, ένα σώμα του ηλιακού συστήματος
Η Αντιγή (Αντίχθων) ήταν, σύμφωνα με τον Φιλόλαο, ένα σώμα του ηλιακού συστήματος
με μάζα ίση με αυτή της Γης, σε τροχιά γύρω από το Κεντρικό Πυρ. Η Αντιγή δεν είναι ορατή
από τη Γη επειδή βρίσκεται κάθε φορά στην αντίθετη θέση, είτε είναι βράδυ (αριστερά)
είτε είναι μέρα (δεξιά). Πηγή: Wikimedia Commons
v
Ο Φιλόλαος θα προχωρήσει ένα βήμα πιο πέρα. Σύμφωνα με τον Αέτιο (ΙΙ, 7, 7) υποστήριξε ότι η Γη δεν βρίσκεται στο κέντρο του κόσμου, ο οποίος κινείται εν πομπή γύρω από μια αόρατη Κεντρική Φωτιά, την οποία αποκαλούσε «εστία του παντός, σκοπιά του Δία (Διός φυλακή), μητέρα των θεών, βωμό, συνεκτικό δεσμό και μέτρο της φύσης». Αν και μιλά για έναν «πνευματικό ήλιο», αυτή η κοσμολογική ενόραση είναι που θα οδηγήσει τον Κοπέρνικο να εκφέρει την επαναστατική υπόθεση του ηλιοκεντρισμού, όπως δήλωσε ο ίδιος στην αφιέρωσή του στον Πάπα Παύλο Γ΄. Γύρω από το κεντρικό πυρ περιφέρεται επίσης το δέκατο αόρατο ουράνιο σώμα, η Αντιγή (Αντίχθων), η ύπαρξη της οποίας εικαζόταν από τους πυθαγόρειους προκειμένου να πληρωθεί η Δεκάδα των ουρανίων σφαιρών.
Μπορεί κάποιος να πει ότι η υπόθεση αυτή ήταν ευφάνταστη ή αφελής. Τι θα πει όμως όταν μάθει ότι ο Λε Βεριέ, και κατόπιν ο Λόουελ, θα ανακαλύψουν στη θέση αυτή το 1846 τον Ποσειδώνα, και το 1930 τον Πλούτωνα, χρησιμοποιώντας απλώς τους υπολογισμούς των πυθαγορείων;
v
Το τέλος των Πυθαγορείων
Οι Πυθαγόρειοι μίλησαν για όλα σχεδόν τα πράγματα της ζωής: για το ημερολόγιο, την ιατρική, την διαιτητική, τη φαρμακολογία, τη μακροβιοτική, την ευγονική, τη ναυτιλία, την φιλοσοφία, την ηθική κάθαρση, την ψυχολογία, τις φυσικές επιστήμες, τη μεταφυσική, την άθληση, τη μαντική, τη θεολογία, την πολιτική. Είναι αδύνατο να υπεισέλθει κάποιος σε όλα αυτά τα θέματα, για τα οποία υπάρχει εκτεταμένη βιβλιογραφία. Σε πολλά από αυτά οι απόψεις τους όχι μόνο δεν έχουν ξεπεραστεί –λόγου χάρη στο ζήτημα της ψυχής– αλλά χρειάζεται μάλλον ένας πιο προχωρημένος πολιτισμός από τον δικό μας για να γίνουν πλήρως αντιληπτές.
Όλη αυτή η επαναστατική δραστηριότητα, που άρχισε να μεταβάλλει την όψη του κόσμου, δεν μπορούσε να περάσει απαρατήρητη. Η σύγκρουση με τις δυνάμεις της οπισθοδρόμησης και του σκότους, που θέλουν τους ανθρώπους σε ληθαργική κατάσταση ώστε να είναι εύκολα χειραγωγήσιμοι, ήταν αναπόφευκτη. Στην έχθρα κατά του προσώπου του Πυθαγόρα, συνέβαλαν και τα κοινολογηθέντα μυστικά από τους μαθητές των κατώτερων βαθμίδων, πολλά από τα οποία ήταν αποκυήματα της φαντασίας τους. Το ίδιο συνέβαλε και η αυστηρότητα της επιλογής των μελών του Ομακοΐου, όπως ονομαζόταν η σχολή που διατηρούσε ο Πυθαγόρας στον Κρότωνα.
Ένας πλούσιος ευγενής, ονόματι Κύλων, ο οποίος είχε απορριφθεί από τη σχολή, οργάνωσε από φθόνο ένα αντιπυθαγορικό κίνημα, στρατολογώντας υποανάπτυκτα άτομα. Υπήρξε τέτοιος φανατισμός, ώστε οι οπαδοί περικύκλωσαν και έβαλαν φωτιά στο οίκημα όπου συνεδρίαζαν οι πυθαγόρειοι. Όλοι κάηκαν, εκτός από δύο, ενώ η έκταση του κινήματος, λόγω της ολιγωρίας των αρχών των πόλεων, έλαβε τέτοια μορφή, ώστε παντού στη Μεγάλη Ελλάδα να γίνονται εμπρησμοί στα μέρη όπου συνεδρίαζαν οι πυθαγόρειοι. Ο ίδιος ο Πυθαγόρας με την οικογένειά του κατέφυγαν, κατά μια εκδοχή, στη Σύρο, κοντά στον Φερεκύδη, ενώ κατ’ άλλη, στο Μεταπόντιο. Και ενώ οι πυθαγορικοί σύλλογοι άρχισαν να φθίνουν και να εξαφανίζονται, η σεβάσμια μορφή του μεγάλου δασκάλου και μύστη, έχοντας περιβληθεί το φωτοστέφανο της αιωνιότητας, ζει από γενιά σε γενιά μέχρι τις μέρες μας.
v
Η αθανασία της ψυχής
Η μικρή αυτή μελέτη δεν θα ήταν αρτιμελής αν παραλείπαμε να αναφερθούμε, ακροθιγώς έστω, στη θεωρία της ανακύκλησης των ψυχών. Θα επικεντρωθούμε σε τρεις παρατηρήσεις του Αλκμαίωνα, του γιατρού και φιλοσόφου τον οποίο ο Διογένης Λαέρτιος και ο Ιάμβλιχος θεωρούν ότι υπήρξε μαθητής του Πυθαγόρα. Την πρώτη την αναφέρει ο Αριστοτέλης (Περί ψυχής Α 2, 405 a 29):
παραπλησίως δε τούτοις και Αλκμαίων έοικεν υπολαβείν περί ψυχής∙ φησί γαρ αυτήν αθάνατον είναι διά το εοικέναι τοις αθανάτοις∙ τούτο δ’ υπάρχειν αυτή ως αεί κινουμένη∙ κινείσθαι γαρ και τα θεία πάντα συνεχώς αεί, σελήνην, ήλιον, τους αστέρας και τον ουρανόν όλον.
«Φαίνεται ότι και του Αλκμαίωνα η άποψη περί ψυχής είναι παραπλήσια με τις αντιλήψεις εκείνων (δηλαδή του Θαλή, του Διογένη Απολλωνιάτη και του Ηράκλειτου)∙ γιατί ο Αλκμαίων λέει ότι η ψυχή είναι αθάνατη, λόγω της ομοιότητάς της με τα αθάνατα∙ και έχει αυτή την ιδιότητα επειδή είναι πάντα σε κίνηση∙ γιατί όλα τα θεία κινούνται συνεχώς – η σελήνη, ο ήλιος, τα άστρα και όλο το στερέωμα».
Τη δεύτερη την αναφέρει ο Αέτιος (IV, 2, 2):
Αλκμαίων φύσιν αυτοκίνητον κατ’ αΐδιον κίνησιν και διά τούτο αθάνατον αυτήν και προσεμφερή τοις θείοις υπολαμβάνει.
«Ο Αλκμαίων υποθέτει ότι η ψυχή είναι μια ουσία που κινείται από μόνη της αέναα, και γι’ αυτό το λόγο αθάνατη και παρεμφερή με τα θεία».
Η τρίτη αναφέρεται στο έργο Προβλήματα που αποδίδεται στον Αριστοτέλη (ΧVII, 3, 916 a 33):
τους ανθρώπους φησίν Αλκμαίων διά τούτο απόλλυσθαι, ότι ου δύνανται την αρχήν τω τέλει προσάψαι.
«Ο Αλκμαίων λέει ότι οι άνθρωποι πεθαίνουν επειδή δεν μπορούν να ενώσουν το τέλος με την αρχή».
 «Ο άνθρωπος πεθαίνει επειδή αποτυγχάνει να ενώσει το τέλος με την αρχή» (Αλκμαίων).
«Ο άνθρωπος πεθαίνει επειδή αποτυγχάνει να ενώσει το τέλος με την αρχή» (Αλκμαίων).
Ουροβόρος όφις με την επιγραφή «Εν το παν» από το βιβλίο Χρυσοποιία της Κλεοπάτρας
της Αλχημίστριας (3ος-4ος αι. μ.Χ.). Πηγή: Wikimedia Commons
v
Στο πρώτο και στο δεύτερο απόσπασμα έχουμε ένα σαφές επιχείρημα για την αθανασία της ψυχής. Παρόμοια επιχειρήματα έχουν αναπτύξει ο Πλάτωνας και ο Αριστοτέλης (Περί ψυχής), εδώ όμως έχουμε για πρώτη φορά το πέρασμα από το αξίωμα ότι η ψυχή κινείται συνεχώς στο συμπέρασμα ότι είναι αθάνατη. Τα ουράνια σώματα αναφέρονται απλώς ως ενισχυτική αναλογία.
Το αξίωμα ότι η ψυχή κινείται αέναα βασίζεται ίσως στη σκέψη ότι μόνο τα έμψυχα όντα κινούνται από μόνα τους, επειδή ακριβώς έχουν ψυχή. Αν όμως η ουσία της ψυχής είναι η αυτοκίνηση, η ψυχή δεν μπορεί ποτέ να πάψει να κινείται και, συνεπώς, δεν μπορεί ποτέ να πάψει να ζει: άρα λοιπόν είναι αθάνατη (παρβλ. Φαίδρος 245 c – 246 a, ένα χωρίο που προφανώς είναι εμπνευσμένο από τον Αλκμαίωνα).
Το τρίτο απόσπασμα είναι πιο δύσκολο να ερμηνευθεί. (Αυτό ωστόσο δεν εμπόδισε να αναπτυχθεί μια ολόκληρη επιστήμη, αν μπορούμε να την αποκαλέσουμε έτσι, με στόχο την αναζήτηση της αθανασίας, η οποία στους αλεξανδρινούς χρόνους πήρε τη μορφή της γνωστής μας αλχημείας, με κυρίαρχο σύμβολο τον ουροβόρο όφι – το φίδι που τρώει την ουρά του).
Ίσως εδώ ο Αλκμαίων υπαινίσσεται ότι ο τρόπος με τον οποίο τα ουράνια σώματα συνεχίζουν ασταμάτητα την κίνησή τους, δηλαδή η επανάληψη των περιστροφών τους, είναι ανέφικτος για τον άνθρωπο, επειδή η διαδικασία του γηρασμού δεν είναι αντιστρεπτή. Ένας άνθρωπος δεν μπορεί να γίνει από γέρος μωρό («δεν μπορεί να ενώσει το τέλος με την αρχή»), όσο είναι κλεισμένος στο ίδιο σώμα. Αν λοιπόν είναι αθάνατος, όπως μας διδάσκουν τα προηγούμενα χωρία, πρέπει να υποστεί φυσικό θάνατο και να ακολουθήσει η μετενσάρκωσή του σε ένα νέο σώμα…
Σημείωση στον Λε Κορμπυζιέ
Ενώ αρχικά το ανθρώπινο Modulor βασιζόταν στα 1,75 μέτρα, όσο το μέσο ύψος ενός άνδρα, με παρέμβαση του Λε Κορμπυζιέ μεγάλωσε το 1946 στα 1,83 μέτρα. Ταυτόχρονα, το ύψος ενός όρθιου άνδρα με το χέρι σηκωμένο ψηλά, ορίστηκε στα 2,26 μέτρα (όσο δηλαδή το ύψος σήμερα μιας πόρτας).
Η γραφική κλίμακα του Λε Κορμπυζιέ, που αποτελεί πλέον τη βάση της σύγχρονης κατασκευαστικής σε ολόκληρο τον πλανήτη, περιλαμβάνει μια στυλιζαρισμένη ανθρώπινη φιγούρα με το ένα χέρι σηκωμένο ψηλά, που στέκεται δίπλα σε δύο κάθετες μετρήσεις: στην κόκκινη σειρά, με βάση το ύψος του ομφαλού της μορφής (1,08 μ. στην αρχική έκδοση του αυτοκρατορικού μετρικού συστήματος, 1,13 μ. στην αναθεωρημένη έκδοση από τον Λε Κορμπυζιέ), και στην μπλε σειρά που βασίζεται στις αναλογίες που προκύπτουν από ολόκληρο το ύψος της ανθρώπινης μορφής, που αποτελεί διπλασιασμό του ύψους του ομφαλού (2,16 μ. στην αρχική έκδοση, 2,26 μ. στην αναθεωρημένη). Η σπείρα που αναπτύσσεται γραφικά μεταξύ των κόκκινων και μπλε τμημάτων, μιμείται την ένταση της ανθρώπινης μορφής.
Έτσι, σήμερα στους πολεοδομικούς κανονισμούς διαβάζουμε ότι για να είναι κατοικήσιμο ένα δωμάτιο, το ύψος του δεν πρέπει να είναι μικρότερο από 2,60 μέτρα, ενώ στην περίπτωση επικλινούς στέγης, όχι μικρότερο από 1,83 μέτρα, με το μέσο ύψος του χώρου όχι μικρότερο από 2,60 μέτρα. Το ιδεώδες βέβαια ύψος είναι τα 3,20 μέτρα.
v
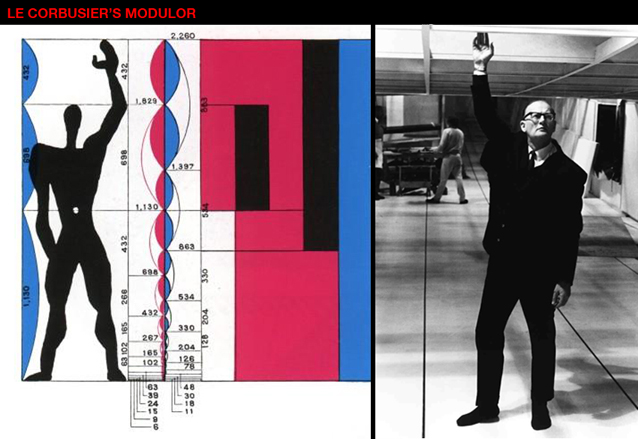
Το Modulor είναι η ανθρωπομετρική κλίμακα αναλογιών που επινοήθηκε από τον Ελβετό αρχιτέκτονα Λε Κορμπυζιέ (1887-1965) με βάση την Χρυσή Τομή. Αναπτύχθηκε αρχικά ως μια οπτική γέφυρα ανάμεσα σε δύο ασύμβατα μεταξύ τους μετρικά συστήματα, το αυτοκρατορικό βρετανικό σύστημα του 1824 που είχε υιοθετηθεί από τους Αμερικανούς και το γαλλικό μετρικό σύστημα του 1799. Βασίζεται στο ύψος ενός ανθρώπου με το χέρι σηκωμένο ψηλά, όπως δείχνει ο ίδιος ο Λε Κορμπυζιέ (δεξιά).
v
Το 1946, ο Λε Κορμπυζιέ επισκέφθηκε τη Νέα Υόρκη, όπου συναντήθηκε με τον Henry J. Kaiser, έναν Αμερικανό βιομήχανο ο οποίος είχε ναυπηγήσει τα περίφημα Λίμπερτυ κατά τη διάρκεια του Β΄ Παγκοσμίου Πολέμου. Συζητώντας, ο Kaiser παραπονέθηκε στον Λε Κορμπυζιέ ότι το μεγαλύτερο πρόβλημα που είχε αντιμετωπίσει στην κατασκευή των Λίμπερτυ, που επρόκειτο να μεταφέρουν εφόδια για τα αμερικανικά και βρετανικά στρατεύματα στην Ευρώπη, αφορούσε το διαφορετικό μετρικό σύστημα των δύο ηπείρων. Ο Λε Κορμπυζιέ προθυμοποιήθηκε τότε να φτιάξει (στην πραγματικότητα να προωθήσει, γιατί την είχε ήδη έτοιμη) μια αρμονική κλίμακα, βασισμένη στις αναλογίες της Χρυσής Τομής, που θα γινόταν παγκόσμιο μέτρο. Έτσι και έγινε.
Σήμερα, από ένα αεροπλάνο έως τα βιβλία και τα περιοδικά ή το ύψος ενός μπουκαλιού μπύρας μέχρι τις διαστάσεις των κιβωτίων μεταφοράς τους, καθώς και όλα τα υπόλοιπα προϊόντα που παράγονται στον πλανήτη βασίζονται στο Modulor του Λε Κορμπυζιέ.
ν
© 2016 Youmagazine.gr