Ο πιο παλιός και πιο ακριβής τριγωνομετρικός πίνακας
ΑΡΧΑΙΟΛΟΓΙΑ
Posted by Youmagazine Staff
Μια βαβυλωνιακή πινακίδα 3.700 ετών περιέχει τον παλαιότερο και πιο ακριβή τριγωνομετρικό πίνακα στον κόσμο.

Αυτός ο βαβυλωνιακός πίνακας από άργιλο ηλικίας 3.700 ετών φυλάσσεται στη βιβλιοθήκη σπάνιων βιβλίων και χειρογράφων στο Πανεπιστήμιο Κολούμπια της Νέας Υόρκης. Image: Supplied
ν
ΕΝΑΣ μυστηριώδης βαβυλωνιακός πίνακας από ψημένη άργιλο, που περιείχε μαθηματικές πράξεις σε σφηνοειδή γραφή και μεταφράστηκε πρόσφατα από Αυστραλούς ερευνητές, αποδείχθηκε ότι είναι ο παλαιότερος και πιο ακριβής τριγωνομετρικός πίνακας στον κόσμο.
Ο πίνακας, γνωστός ως Plimpton 322, ανακαλύφθηκε στο νότιο Ιράκ στις αρχές της δεκαετίας του 1900 και έως τώρα και έως τώρα παρέμενε αμετάφραστος, καθώς κανείς δεν μπορούσε να καταλάβει τι αντιπροσώπευαν οι μαθηματικές πράξεις που περιείχε.
Πρόσφατα, ο δρ. Ντάνιελ Μάνσφηλντ (Daniel Mansfield) της Σχολής Μαθηματικών και Στατιστικής του Πανεπιστημίου της Νέας Νότιας Ουαλίας (UNSW) στο Σύδνεϋ της Αυστραλίας, κατάφερε να λύσει το μυστήριο, αποδείχνοντας ότι ήταν ένας τριγωνομετρικός κώδικας, που τον χρησιμοποιούσαν οι αρχαίοι μαθηματικοί για να υπολογίσουν πώς να κατασκευάσουν παλάτια και ναούς και να χτίσουν κανάλια.
«Η πινακίδα Plimpton 322 προβληματίζει τους μαθηματικούς εδώ και 70 χρόνια, καθώς δεν είχαν συνειδητοποιήσει ότι περιέχει ένα ειδικό πρότυπο αριθμών που ονομάζεται “Πυθαγόρεια τριάδα” (Pythagorean triple)», δήλωσε ο δρ. Μάνσφηλντ.
ν

Ο δρ. Ντάνιελ Μάνσφηλντ με την βαβυλωνιακή μαθηματική πινακίδα Plimpton 322 στη βιβλιοθήκη σπάνιων βιβλίων και χειρογράφων στο Πανεπιστήμιο Columbia της Νέας Υόρκης. Πηγή: UNSW / Andrew Kelly
ν
Μια Πυθαγόρεια τριάδα αποτελείται από τρεις θετικούς ακέραιους αριθμούς α, β, και γ, ώστε να ισχύει η σχέση α2 + β2 = γ2, σχέση που είναι ευρέως γνωστή ως Πυθαγόρειο θεώρημα. Μια τέτοια τριάδα συνήθως γράφεται α, β, γ και ένα χαρακτηριστικό παράδειγμα αποτελούν οι αριθμοί 3, 4, 5, εφόσον ισχύει 32 + 42 = 52. Εάν α, β, γ είναι πυθαγόρεια τριάδα, τότε ομοίως θα είναι και η κα, κβ, κγ για οποιοδήποτε θετικό ακέραιο κ.
ν
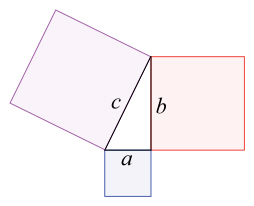
Το πυθαγόρειο θεώρημα: a2 + b2 = c2
ν
Μια πρωτογενής πυθαγόρεια τριάδα είναι αυτή στην οποία οι α, β, γ είναι πρώτοι μεταξύ τους (δηλαδή ο μέγιστος κοινός διαιρέτης των α, β, γ είναι το 1).
«Η πινακίδα», εξηγεί ο δρ. Μάνσφηλντ, «δεν περιέχει μόνο τον παλαιότερο τριγωνομετρικό πίνακα στον κόσμο. Είναι επίσης ο μόνος εντελώς ακριβής τριγωνομετρικός πίνακας, λόγω της πολύ διαφορετικής βαβυλωνιακής προσέγγισης της αριθμητικής και της γεωμετρίας».
Ο δρ. Μάνσφηλντ έψαχνε υλικό για να το χρησιμοποιήσει στην τάξη όπου διδάσκει μαθηματικά, όταν έπεσε πάνω στην βαβυλωνιακή πινακίδα «εντελώς τυχαία».
«Είδα, όπως και οι άλλοι μαθηματικοί, ότι επρόκειτο για κάποιο είδος τριγωνομετρίας, αλλά δεν μπορούσα να καταλάβω πώς λειτουργεί. Έτσι, άρχισα να το ψάχνω. Ομολογώ ότι μεγάλη βοήθεια μου πρόσφεραν οι προηγούμενες μελέτες του καθηγητή Νόρμαν Γουάιλντμπεργκερ (Norman Wildberger). Ο καθηγητής είχε κάνει προηγουμένως αρκετή δουλειά πάνω στην τριγωνομετρία του πίνακα που βασιζόταν σε αναλογίες, αντί σε γωνίες και κύκλους όπως σήμερα – και αυτό αποδείχθηκε ότι ήταν το κλειδί για το σπάσιμο του κώδικα».
«Το θέμα ήταν το δεις το σύνολο του πίνακα με διαφορετικό μάτι. Τότε όλα μπήκαν στη θέση τους», καταλήγει ο δρ. Μάνσφηλντ.
Η έρευνα του δρα Μάνσφηλντ για το σπάσιμο του κώδικα διάρκεσε δύο χρόνια.
Εάν οι υπολογισμοί του Αυστραλού μαθηματικού είναι σωστοί, αυτό σημαίνει ότι οι Βαβυλώνιοι και όχι οι αρχαίοι Έλληνες ήταν οι πρώτοι που μελέτησαν την τριγωνομετρία –την επιστήμη των τριγώνων– έστω και με διαφορετικό τρόπο. Αλλά αυτό μένει να αποδειχτεί.







